A Framework for Understanding Options:
Defining Their Payoffs and Risks
by Rich Tanenbaum

(from Topics in Money and Securities Markets, Bankers Trust Company, Money Market Center, April 1987)

INTRODUCTION

It's happened to virtually every investor. Trying to ride a market rally just a little too long. Or maybe waiting for that correction to turn around...and waiting...and waiting...

All humans have an innate ability to be wrong sometimes. Wouldn't it be nice to contain our losses in those situations, and still make money when we're right? Well, we can, thanks to options products.

This paper briefly examines the basic concepts underlying options, provides some examples of their uses, and introduces the "payoff diagram," a relatively simple, graphic way to calculate the risks and rewards associated with various option strategies. These diagrams can be a convenient and useful tool for taking advantage of the rapidly growing options markets. Some examples of how options can be used to redistribute risk or take advantage of market opinions are given along the way.

Are Options "Difficult"?

Options can seem like complex securities, perhaps because there are so many of them and because they have a wide range of application. Yet they are not much more complicated than other financial instruments encountered regularly. So why do many people find them so confusing? The uneasiness may reflect the fact that there are some sophisticated and complex financing and investment strategies that flow from their use. Once the basic concept is understood, however, those strategies become much easier to grasp.

For example, risk can be hedged in a variety of ways. In some instances, a successful overall investment strategy can be fined-tuned to assure a minimum payoff; similarly, losses can be contained. Options can be used in more traditional corporate borrowing or to accomplish some unusual types of financing, for example where both the borrower and the lender are willing to bear some risk in the hope of greater rewards.

Just What is an Option?

An option is a security that permits the holder to execute a transaction in the future at a price determined today. This is similar to a forward contract, except that, unlike a forward, the option holder can decide in the future whether or not he still wants to complete the transaction.

There are two types of options. A call option permits the holder to buy something in the future. A put option permits the holder to sell something in the future.

A simple way to remember the difference is to recall that an option gives its buyer the choice of entering into a transaction with another party in the future. The buyer of the option puts up the money today for that choice; the option writer must then comply with the option buyer's decision. The transaction can either be the option holder's right to buy something at a specified price (a call option), or to sell something at a specified price (a put option).

EXAMPLES OF USING OPTIONS

Speculation

Suppose a foreign exchange trader is considering buying yen for delivery one year forward. If she knew that spot yen in a year was going to be trading below the current forward price, she would never agree to buy yen forward today. Similarly, if she knew spot yen was going to be trading above today's one year forward, she would buy as much yen forward as possible.

Lacking a clairvoyant advisor, she can buy a call option on yen that expires in a year. This call option gives the holder the right to buy a specific asset (yen) on a certain date (a year from now) at a specified price (the strike price). Then, if yen is trading above the strike price of the option a year from now, the trader can exercise the call option and buy yen at the strike, saving the difference. If yen is trading below the strike, she simply lets the option expire and buys yen in the spot market more cheaply.

This example can also be applied to puts. If she knew spot yen would be trading in a year more cheaply than today's forward price, she might want to sell it forward today. However, if she was wrong, she'd be delivering yen at what would turn out to be an unfavorable price. By buying a put today, she can have the right to sell yen in a year. If the strike price turns out to be favorable, she will exercise her option and complete the second transaction. Conversely, should yen strengthen in a year, she will choose not to exercise her option.

Hedging a Borrowing

As another example, assume a corporate treasurer knows that in a year his company will need to borrow $1 million for five years. He wants to be able to obtain today's low interest rates. Not confident in picking the absolute low point in rates, the treasurer also would like to take advantage of any further rate decline. By entering into an agreement to issue a bond in a year and simultaneously buying an option to call that bond back at par at the time of issue, the borrower can indeed have the best of both worlds. If interest rates in a year are below the strike rate of his option, he exercises the option and issues a new bond at the lower rate. If rates are higher, he issues the original bond and simply lets the option expire.

The standard choices: waiting a year, or entering into a forward rate agreement today; lock the treasurer in at possibly unfavorable rates. Waiting will hurt should rates fall (of course the option, while delivering the best of both worlds, costs something, so the choice is not as clear-cut as it might seem).

This example is similar to a callable bond, with which you are probably already familiar. These are standard bonds, but the issuer also has bought a call option from the investor to buy the bond back at specified prices (the call prices) on specified dates (the call dates).

Note here that the corporation is transferring its risk of changing rates to the seller of the call option. Options perform a social good by allowing us to reallocate our risk to those who can supposedly best bear it. If the call option writer had himself bought a call option from somewhere else, for whatever reason, the writing of the call option to the corporation actually results in a net reduction in his risk, also.

Capital Preservation

Consider a long term bond originally purchased at 95 and now trading at 120. The buyer remains optimistic about the bond market, but would hate to hold on only to see rates rise rapidly and profits disappear. This is a job for a put option. If the investor buys the right to sell the bond at 120 in six months, then he will be guaranteed not to lose any current principal on the trade over a full half year. This is so because if the market rises, he has caught the uptrade, but if the market falls, say to 105, he exercises the put and sells the bond at 120.

The put option does carry a cost, probably about 4% of principal. If the investor is willing to buy a put with a strike of 116 instead of 120, then the option premium is less, probably about 2.5%, but he then runs the risk of losing a portion of his profits because he can only sell the bond at 116 or higher. Similarly, he could insure his gains over a year rather than six months. This will cost a little more, but he receives a little more.

Covered Call

Another example is the covered call. This position is popular with portfolio managers who already own a bond and want to earn some extra income. By writing a call option against the bond, they receive income today in the form of the option premium, or cost, of the option. If the option's strike is significantly above the current bond price, then in the absence of a large rally they will just keep the premium, and the option will never be exercised. And if the market does rally, they will still participate in some of the gain, selling the bond at the strike (while still having received the option premium).

Capital Preservation Without All the Upside

This is yet another technique for hedging risk. Suppose again an investor had bought a bond at 95, watches it rise to 120 and now buys a 120 put. But this time he simultaneously writes a 130 call. The up-front cost is less, because someone is paying the investor for the call (he might pay 4 for the put, and receive 1 for the call, for a net cost of 3), but if the bond goes above 130 someone is going to buy it from him. Since the bond is trading at 120 now, profit so far is 25. The final payoff would be:

• if the bond goes down, it can be sold at 120, locking in a profit of 25 on the bond, less the options' cost of 3, for a net profit of 22;
• if the bond rises a little, say to 123, net profit will be 28 minus 3, or 25;
• if the bond rises sharply to 140, say, the investor will be forced to sell it at 130 (the call will be exercised) for a profit of 35 on the bond, less the options' cost of 3, or 32 total.

This strategy is attractive for those who want to pay less today to lock their book profits, and are willing to forego the possibility of realizing huge gains later.

Straddles

As another example, take a trader in the British pound. Because of the volatile oil situation, he thinks the pound is going to move sharply over the next two months. The only problem is he is unsure of the direction. Normally, this would make him the laughing stock of the trading desk. Thanks to options, though, the trader can benefit no matter what the outcome. With the pound at 1.45, he can buy a 1.60 call and a 1.30 put.

Each of these will carry an initial cost, probably about $0.04 per pound for the two of them. However, when the options expire, if the pound is trading at 1.70, the trader will have $0.10 in his pocket. This comes from the fact that he can buy the currency at 1.60 by exercising his call, and turn around and sell it at 1.70.

This 0.10 profit is termed the "intrinsic value" of the option. For a call it is what can be realized by exercising the option and then selling the underlying asset. The intrinsic value of a put is the amount that can be realized by buying the asset, and immediately exercising the put option. If the transaction would not cause the option holder to profit, the intrinsic value is zero.

Continuing with the example, if the pound drops to 1.10, he will have 0.20 by exercising the put. A little rumination shows that in any scenario in which the pound is trading outside the range of 1.30 to 1.60 at expiration, one of the options is valuable ("in the money"), and the other one is worthless ("out of the money"). The intrinsic value of the in the money option is equal to the difference between the spot pound and the option's strike. Thus, the more the pound moves, the more the trader earns. The direction makes no difference. The trader has straddled the market. Of course, if the pound is trading between 1.30 and 1.60, both options will expire worthless, and the trader will be the laughing stock of the desk.

This example is used by some to illustrate that options are most useful in dynamic and volatile markets; that they are for people who love risk. However, if the trader's view had instead been that the pound was going to remain in the 1.30-1.60 range, he could have sold the put and the call (sold the straddle), receiving the premium, and hopefully never being exercised against. This example is used by some to illustrate that options are most useful in quiet and stable markets. Some would also call the strategy that buys both options very risky, because the entire investment can be lost. Others term it very safe, because the maximum loss is defined up front.

There are any number of variations on the theme illustrated with the pound. The trader can choose any time horizon. The range is subject to alteration, too. It doesn't have to be equidistant from today's spot price, as was the case in the example. In fact, the range could be completely above or below the spot price.

Obviously, the trade need not be done in the pound. We could have chosen not only other currencies, but also any entity that trades. For instance, a trader can put on a position that will make money whenever the slope of the yield curve becomes either very positive or very negative.

THE PAYOFF DIAGRAM

Even if we stick to one strategy, it can be applied in a number of ways: different strikes, time horizons, underlying assets, etc. If we were to list them all, and then talk about another strategy, and another, this paper would be very long, indeed.

Since a picture is worth a thousand words (give or take a few), we can save time by representing options with graphs. Not only will this save space and time, it will make the concepts easier to grasp. Our vehicle of representation is the "payoff diagram," which (at this point) can be defined as a graph that represents the monetary value on an option position at expiration, given different values of the underlying asset.

Long Call

Let's take a call. If you bought a six month call on a 30 year bond with a strike of 120, what would the value of the option be at expiration? The answer is shown in Table 1.

Table 1: Value of a 120 Call Under Different Bond Price Scenarios
Bond Price	Call Value
90	0
100	0
110	0
120	0
125	5
130	10

A pattern emerges; whenever the bond is trading below 120, the option is worthless. Whenever it is trading above 120, it is worth the bond price minus 120, or intrinsic value. The payoff diagram is shown in Figure 1:

Observe that there are two lines. The first is flat, parallel to the x axis. This corresponds to the bond finishing below 120. The other line slopes upward. Here, for every one point increase in the underlying bond, the option value rises by one point. This one-to-one correspondence means the slope of this line is one. Notice that the lines intersect at 120, which is the strike price.

We should be a little more precise, though, and recognize that we paid something for the call. If the cost was 3, a more accurate picture would be that of our profit and loss, as shown in Figure 2.

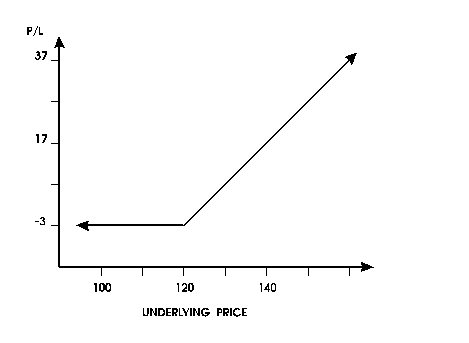
This graph looks just like the last one, with one difference; both lines have been lowered 3 points to reflect the purchase price.

If we instead looked at a 115 call costing 5, we will get the payoff diagram shown in Figure 3. The shape is the same, but the lines meet in a different spot.

Rather than graph every possible call, it will be easier to remember that the general payoff diagram of a call has two lines: the left one is horizontal, the right one has a slope of one, and they intersect at the strike price. The horizontal line passes through the P/L axis at the negative of the option cost.

Table 2: Profit and Loss on a 1.30 Pound Put
When the pound ends up at:	You will have:	For a profit/loss of:
1.00	0.30	0.28
1.20	0.10	0.08
1.40	0.00	-0.02
1.60	0.00	-0.02
1.70	0.00	-0.02

Long Put

Let's produce some pound put pictures. If one buys a 1.30 put on Sterling at a price of .02, the table of the value of the put would be as illustrated by Table 2. This can be translated into the graph shown in Figure 4.

After drawing a few of these, it becomes apparent that a general graph for puts may be drawn. It too has two lines. For a put, the left one slopes downward from upper left towards lower right, and the right is flat. Like a call, they intersect at the strike price, and the line, if extended, would intersect the P/L axis at the negative of the option premium.

Short Positions

Options are a zero-sum game. That means that an option buyer's gain is the seller's loss, and vice versa (ignoring commissions). Because of this, the payoff diagram of the dollar return from owning an option must be the mirror image of the seller's profit and loss. Whenever the previous payoff diagram are positive (negative), the payoff of a short position in the same option will be negative (positive). For example, the table for a short position in a 1.30 put costing 0.02 is shown in Table 3.

Table 3: Profit and Loss on a Short Position in a 1.30 Put
When the pound ends up at:	You will have:	For a profit /loss of :
1.00	-0.30	-0.28
1.20	-0.10	-0.08
1.40	0.00	0.02
1.60	0.00	0.02
1.70	0.00	0.02

A short put is presented in Figure 5. Note that it is Figure 4 flipped over.

Non-Option Payoff Diagrams

Another payoff diagram of interest is a long position in the underlying asset. If that asset is trading at 100, the long position in the underlying is shown in Table 4.

Table 4: Profit and Loss from Holding the Underlying Security
If the underlying ends up at :	The profit/loss is:
20	-80
50	-50
100	0
125	25

The graph of this is Figure 6.

The tabular representation of holding $100 worth of a one-year U.S. Treasury bill for a year, purchased to yield 6%, is presented in Table 5, with the associated graph presented in Figure 7.

Table 5: Profit Over One Year from Holding a Bill Yielding 6%
If the 'underlying' ends up at:	The profit will be:
20	6
40	6
100	6
1000	6

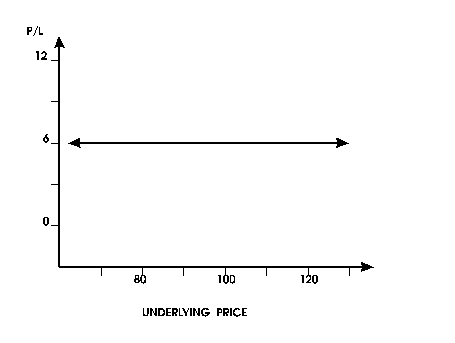
This probably requires a little explanation. The point of the example is that no matter where any asset is trading at expiration, the investment is going to earn 6. There is no underlying asset per se, since there is no option. We can think of the left hand column as gold prices. Wherever it is trading in a year, if you lend money at 6% for a year you will make 6% on your money. No matter what.

Of course, we have short positions in all of these, but they will always be simple mirror images of long positions. We should note here that these graphs are general in the sense that the underlying asset is never identified. These could be DM options just as easily as bond options. In addition, time has implicitly been left of the graphs (except the T Bill) because we are looking at the position value at expiration.

Option Portfolios

With payoff diagrams, we also can look at more complicated option positions. It turns out that the payoff diagram of a complicated option position is just the sum of the payoff diagrams of each component of the position. For instance, we wrote earlier about "straddling" the market when the pound sterling was expected to be volatile. The person who took this position was long both a put and a call. 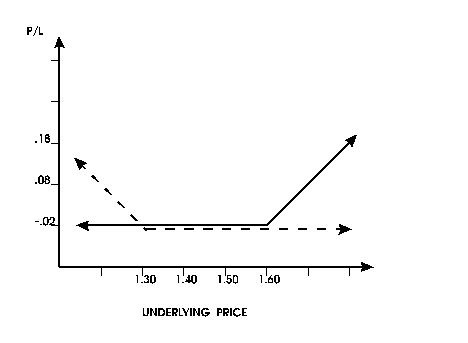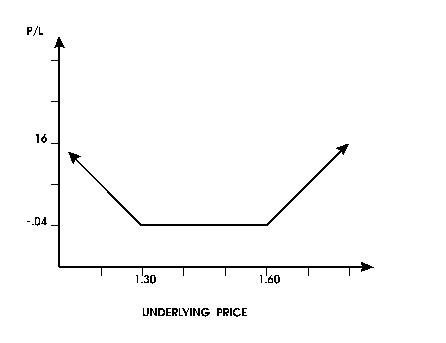The payoff can be graphed by adding together the payoff of a put and a call, and graphing the sum. First, we derive Table 6. The payoff diagram of both the put and the call is shown in Figure 8, and the payoff diagram of the straddle is illustrated by Figure 9.

Table 6: Profit and Loss form Holding a 1.60 Call and a 1.30 Put
Pound rate:	Payoff of call:	Payoff of put:	Cost of call + put:	P&L:
1.10	.00	.20	.04	.16
1.15	.00	.15	.04	.11
1.25	.00	.05	.04	.01
1.35	.00	.00	.04	-.04
1.45	.00	.00	.04	-.04
1.65	..05	.00	.04	.01
1.85	.25	.00	.04	.21

As can be seen, adding the graphs is just as easy as summing the numbers in the table. This way, all we need remember is what the graphs of calls and puts look like. We can combine them in any complex way by just drawing the payoff diagrams of each component of the position, and summing. Thus, a position that is long the underlying, long a 120 put, and short a 130 call, where the net cost of the options is 3, looks like Figure 10.

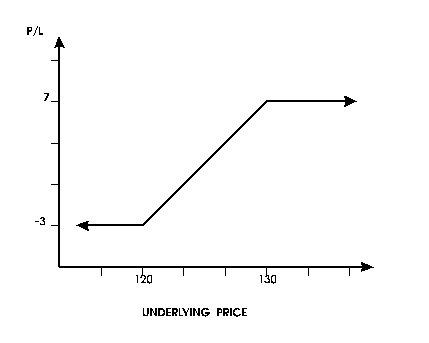
If , as before, we had a 25 point profit to begin with we can just raise the lines by 25 and the graph of total profit would be as shown in Figure 11, which is exactly the same result we stated earlier in this paper:

• a) If the bond goes down, it can be sold at 120, locking in a profit of 25 on the bond, less the options' cost of 3, for a net profit of 22;
• b) If the bond rises a little, say to 123, net profit would be 28 minus 3, or 25;
• c) If the bond rises sharply to 140, say, the investor will be forced to sell it at 130 (the call will be exercised) for a profit of 35 on the bond, less the options' cost of 3, or 32 total.

Thus, using the concept of a payoff diagram not only allows us to simplify the number of combinations of options strategies, but it also makes it easier to assess the implications of each.

ASSESSING RISK AND RETURN

While we can use a payoff diagram to view the possible returns on an option position, it also is useful in examining the riskiness of that position. For instance, knowing what levels the underlying asset must achieve to reach profitability, one can then estimate the probability of reaching those levels. This, then, allows us to systematically state our probabilities of profits and losses, as well as quantify their size. This is a very broad topic, best addressed in a separate paper.

SUMMARY

Heightened volatility in the financial markets and the growing global interaction of those markets have made options an essential element of institutional and corporate portfolios. This is true no matter what opinion one holds on a particular market, be they bull or bear, and regardless of one's appetite for risk, be they lion or lamb.

This paper has defined what options are, provided some examples of their use and introduced a framework for evaluating both individual options and portfolios of options. We also have touched upon ways in which payoff diagrams may be employed to measure risk. There is much more to be said on this topic: how risk and return changes as markets fluctuate. While each of these requires its own thorough treatment, the ideas presented here lay down the fundamentals needed to understand options.